相关基础知识

机器学习

数据

结构化数据、半结构化数据与非结构化数据
- 简单理解：结构化数据是固定键值的，取数据也是固定键值的，例如关系型数据库表；半结构化数据就是有键值，但不固定，可灵活调整键值来取数据，例如JSON格式数据；非结构化数据就是连键值都没有的，例如纯文本、图片等
标记数据与无标记数据

阶段划分

从应用机器学习技术解决业务问题的角度出发，可以分为：

提出问题——数据预处理阶段——特征工程阶段——模型构建和评估阶段

从数据处理完成，到后续分析、应用阶段，可以分为：

分析阶段——训练阶段——测试阶段——应用阶段

数据的不一致性

过拟合
- 分析结果太靠近或者精确匹配一个特定的数据集，从而导致无法适用于其他的数据集
欠拟合
- 模型没有很好训练，导致新年受影响，无法应用于新的数据
解决方法：
- 数据的交叉验证
- 数据修剪
- 数据的正则化等

机器学习算法的分类

按是否需要人工参与数据集的标注，分为：

监督学习
- 给训练数据打上标签，从训练数据中去推导出预测函数，然后用这个函数去预测数据的标签。
无监督学习
- 不需要给训练数据打上标签，从训练数据中去找到隐藏的模式和分组方法，然后用这个来找数据的隐藏结构

从其他角度对机器学习算法进行分类的方法也较多，比如从解决问题的类型出发进行分类，可以有：分类、聚类、回归、降维和密度估计等，暂不展开。

常用的机器学习算法

支持向量机（SVM）
贝叶斯网络（BN）
决策树
随机森林
分层算法/分层聚类算法（HCA）
遗传算法
相似度算法
人工神经网络

机器学习的常用架构

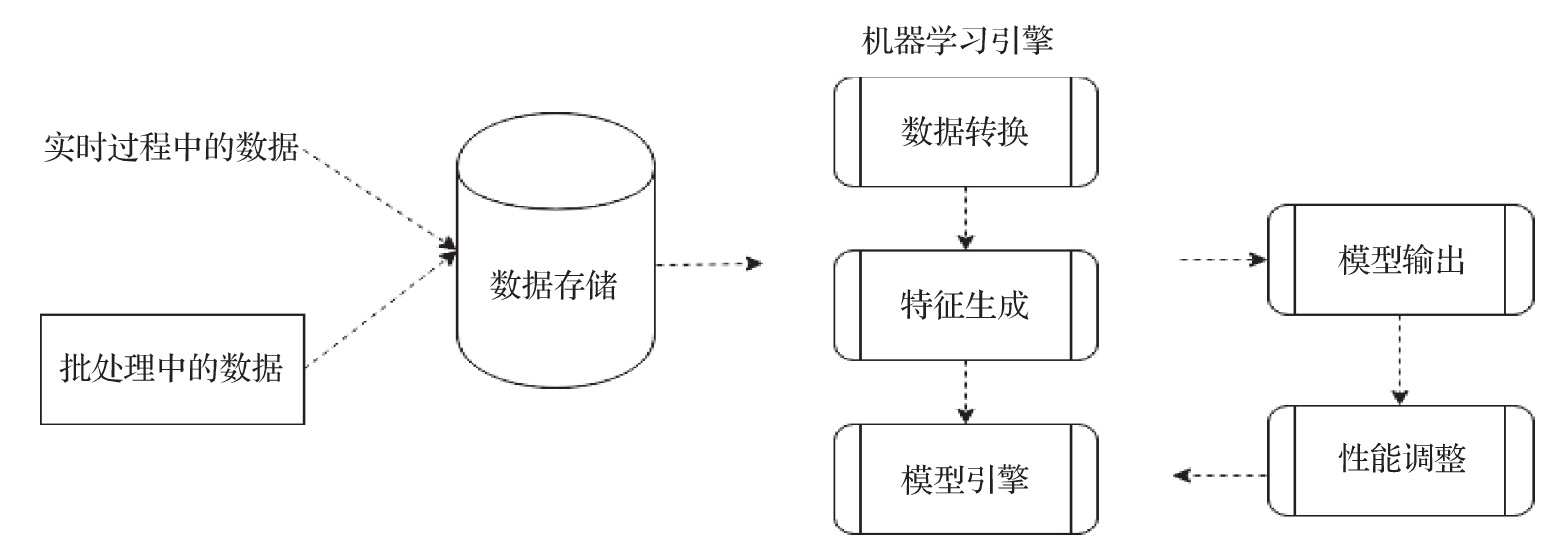
图：典型机器学习系统架构

数据提取
数据存储
模型引擎
- 数据准备
- 特征生成
- 训练
- 测试
性能调整
- 均方误差
- 平均绝对误差
- 精确率、召回率和准确率

模型性能提升方法

获取更多数据
切换机器学习算法
集成多种算法

机器学习环境配置

使用sklearn自带的糖尿病人数据集进行机器学习环境配置的测试，代码文件为：~/source/for_env_test.py，如下：

"""
Author：Toky
Function： 机器学习环境测试
"""

import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt


if __name__ == '__main__':
    # 导入糖尿病数据（sklearn自带）
    diabetes = datasets.load_diabetes()
    """
    展示数据集基本信息
    """
    # # 展示数据集的行数和特征维度数量
    # print(diabetes.data.shape)
    # print(diabetes.feature_names)
    # # 展示数据集描述
    # print(diabetes.DESCR)

    """
    选取所需的特征（本次测试使用个人的BMI指数作为特征）
    """
    diabetes_X = diabetes.data[:, np.newaxis, 3]
    # print(diabetes_X)

    """
    划分数据为训练集和测试集
    """
    # 保留最后20个进行测试
    diabetes_X_train = diabetes_X[:-20]
    diabetes_X_test = diabetes_X[-20:]

    diabetes_y_train = diabetes.target[:-20]
    diabetes_y_test = diabetes.target[-20:]

    """
    训练模型：用训练集数据拟合模型
    测试模型：用测试集数据进行预测
    """
    # 创建线性回归模型
    regr = linear_model.LinearRegression()
    # 使用训练集数据训练模型
    regr.fit(diabetes_X_train, diabetes_y_train)
    # 使用测试集预测标签
    diabetes_y_pred = regr.predict(diabetes_X_test)

    """
    通过均方误差和方差误差的大小来计算拟合度
    """
    mean_squared_error_value = mean_squared_error(diabetes_y_test, diabetes_y_pred)
    print("均方误差为：{0}".format(mean_squared_error_value))
    r2_score_value = r2_score(diabetes_y_test, diabetes_y_pred)
    print("方差误差为：{0}".format(r2_score_value))

    """
    绘制可视化的预测结果
    """
    plt.scatter(diabetes_X_test, diabetes_y_test, color="black")
    plt.plot(diabetes_X_test, diabetes_y_pred, color="blue", linewidth=3)
    plt.xticks(())
    plt.yticks(())
    plt.show()

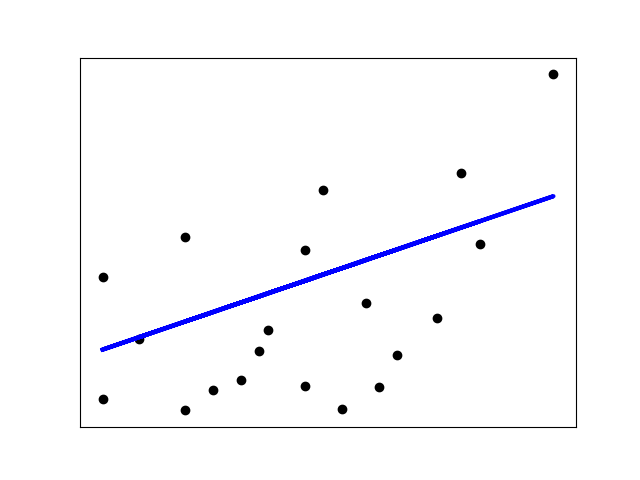
图：预测结果

均方误差为：4058.4102891387315
方差误差为：0.15995117339547205